合格証明証を表示する場所もないので、このエントリに貼り付けていくことにしました。
ちなみに「gacco（統計学／サイエンス／AI・機械学習）の修了証」というページもあります。
ミニぷぱの日本向け公式販売サイトがオープンしたようです。
こちらの公式ツイートによると、2022年6月1日～15日で特別キャンペーンをやっているようです。30％オフとお安く入手できるチャンスです。初日（2022年6月1日？）のみのプレゼントもあるようです。
自分は入手済みなのでもう購入しないですが...。
上記はミニぷぱ「V1」の販売情報ですが、この記事を書いた本日、「V2」の情報が出てきています。詳しくは下記のツイートを参照してください。
Mini Pupper v2 is coming!
— MangDang (@LeggedRobot) 2022年6月1日
With the ears can hear ultrasonic, like a real dog!
With wings can fly, beyond a real dog!
Express your ideas through our Discord https://t.co/IfQv9R13pM
Order Mini Pupper at first,https://t.co/ms066r3OpX pic.twitter.com/CJwBm9FHgq
「Fly in the sky?」とドローン的に飛べるようになるような感じで書かれていますね。AI機能も強化されそうです。以下にV1とV2の比較表を引用しておきます。
これは欲しい。OSは最新のUbuntu 22.04 LTSになり、ミドルウェアのロボット用プラットフォームはROS 2になるようです。V2は年末までにローンチされて出荷開始される計画とのこと。楽しみですね。それまでの練習にV1を購入して、ROSを学んでおくのもよいと思います。ROS 1の知識はROS 2でもある程度有効なようなので。
ミニぷぱV1では下記の2本の記事を執筆しました。これ以上は書く予定はなく、V2待ちです。
これを書くに当たってROSはミニぷぱの開発を試しながら理解していったのですが、下記の書籍『ROSではじめるロボットプログラミング[改訂版] (I/O BOOKS)』を参考にしました（※2021/10/26発売の「改訂版」であることに注意）。
あらためて今日、最初から最後まで読み通しましたが、開発しながらコードや公式ドキュメント、ネット情報から調べて分かったことが全てこの本に書いていました...。本屋さんでこの本を選んだので、これ以外のROS本は読んでいませんが、他の人のコメントを読んでもROS初心者向けの最初の1冊として他の書籍よりもよさそうです。ROS 1を学ぶ人にわたしもお勧めします。
また、上記の2本目の記事もコードコメントの形で重要な内容を含めているので、そちらを読むだけでもROSの理解は広がるかなと思います。
ミニぷぱ（Mini Pupper）のキャリブレーションは意外に失敗しやすいポイントです。ここで失敗するとうまく走行できなかったりこけやすかったりします。実際に私も最初はキャリブレーションに失敗してこけやすく仕上がってしまい、サポートに問い合わせました。
まず、キャリブレーションには、
の2種類の角度があります。PS4版のキャリブレーション時に、公式マニュアル通りにやると45°のキャリブレーションをするようになっていますが、これが難しい。しかし慣れた今ではコツが分かるので紹介します。
あと、PS4版のマニュアル通りにやったつもりでしたが、なぜか90°でキャリブレーションしなければなかったです。これもキャリブレーションに失敗した理由なのですが。
最新のPS4版のソースコードでは45°になっています。個人的には90°がキャリブレーションしやすいと思いましたが、開発元のMangDang社によると「45°が分かりやすい」という意見が多数でこれに決定したとのことでした。
これもかなり慣れてから気付いたこですが、OSイメージをダウンロードできる場所が、
このように複数あります。新しいOSイメージをダウンロードするように気を付けましょう。
具体的には下の図のようになります。図は公式マニュアル「ソフトウェア — Mini Pupper 1.0.0-alpha ドキュメント」から引用した画像を少し加工したものです。
特に重要なのが（1）です。各足の接地点がモーターの軸の完全に真下にすることでこけることがほぼ無くなりました。マニュアルでは45°が強調されていますが、わたしの感想ではこの点が重要で、あとは（2）の関節部分を90°にすればよいだけです。これだけです。45°の分度器は不要です。
もう一方の90°の方は簡単です。具体的には下の図のようになります。図は公式マニュアル「SLAM・ナビゲーション — Mini Pupper 1.0.0-alpha ドキュメント」から引用した画像を少し加工したものです。
単純なキャリブレーションは90°の方が簡単だと思いますが、実際の走行バランスが正確に取れることを考えると、確かに45°でキャリブレーションするのが一番いいですね。
「ミニぷぱの走行バランスがおかしい」「ミニぷぱがこけやすい」という人は、ミニぷぱが静止して起立した状態で、上の45°の状態になっているかを確認してみるとよいと思います。
ミニぷぱでキャリブレーションをしたとき、のPS4版／ROS版ではデータの保存先が異なります。
/home/ubuntu/Robotics/QuadrupedRobot/StanfordQuadruped/calibrate_tool.pyファイルの内容を確認するのが一番良いです。
コードを読むと、Raspberry Pi 4 Model Bボード上のEEPROM（不揮発性メモリ）に格納されています。これにより、PS4版のOSのmicroSDカードを差し替えても、キャリブレーションデータが引き継がれます。
このデータをROS版でも読み取ってくれればよいのですが、ROS版はファイルで管理されているようです。
こちらは/home/ubuntu/catkin_ws/src/minipupper_ros/servo_interface/scripts/calibrate.pyファイルの内容を確認してください。
コードを読むと、/home/ubuntu/catkin_ws/src/minipupper_ros/servo_interface/config/calibration/calibration.yamlファイルとして保存されています。よって、ROS版のOSのmicroSDカードを差し替える場合は、このファイルをコピペすれば引き継げるのではないかと思います（やったことがないので不明）。
どちらかに統一してほしいけど、YAMLファイルの方が取り扱いはしやすいですね。
ROS版にはPS4版のようにGUIで作業できるキャリブレーションツールがありません。PS4版のキャリブレーションツールをROS版で使っても、EEPROMに保存されるだけなので意味がありません。キャリブレーションツールのコードは難しく無さそうなので、ROS版用に修正するということも不可能ではないのですが、そこまでするのは面倒なのですよね。
非常にニッチだと思いますが、ミニぷぱのROS版のGPIOピンの情報を共有します。
※書く必要もないと思いますが念のため。この記事の通りに実施して何か起きた場合の責任は筆者および本サイトは負いません。自己責任でお願いします。
ミニぷぱのROS版でGPIOピンがどのように使われているかはコードを追いかけて調べるしかありません（たぶん、資料がなさそうです）。書き方が雑ですが、自分がコード上に書いたものをコピペしたためです。
自分がコードを調べてチェックした限りでは以下のように使われいるようでした。※勘違いや間違いがあるかもしれないので、あくまでヒントとして参照してください。
# - GPIO0 : ID_SD <Serial Data for HAT for EEPROM> # - GPIO1 : ID_SC <Serial Clock for HAT for EEPROM> # - GPIO2 : I2C SDA <Inter-Integrated Circuit> <Serial Data> # - GPIO3 : I2C SCL <Serial Clock> # - GPIO4 : "[Leg4]Left-Front-Calf" GPCLK0 <General Purpose Clock> # - GPIO5 : "[Leg4]Left-Front-Thigh" GPCLK1 # - GPIO6 : "[Leg4]Left-Front-Hip" GPCLK2 # - GPIO7 : "[Leg3]Right-Back-Calf" SPI CE0 <Serial Peripheral Interface> <Chip Enable> # - GPIO8 : "[Leg3]Right-Back-Thigh" SPI CE1 # - GPIO9 : "[Leg3]Right-Back-Hip" SPI MISO <Master In Slave Out> # - GPIO10: "[Leg2]Left-Fore-Calf" SPI MOSI <Master Out Slave In> # - GPIO11: "[Leg2]Left-Fore-Thigh" SPI SCLK <Serial Clock> # - GPIO12: "[Leg2]Left-Fore-Hip" PWM0 <Pulse Width Modulation> # - GPIO13: "[Leg1]Right-Fore-Calf" PWM1 # - GPIO14: "[Leg1]Right-Fore-Thigh "UART TXD <Universal Asynchronous Receiver Transmitter> <Transmit Data> # - GPIO15: "[Leg1]Right-Fore-Hip" UART RXD <Receive Data> # - GPIO16: "Battery Buzzer" # - GPIO17: # - GPIO18: PCM_CLK <Pulse Code Modulation> <PCM Clock> # - GPIO19: PCM_FS <PCM Frame Sync> # - GPIO20: PCM_DIN <PCM Data In> # - GPIO21: "Servo 2 control" PCM_DOUT <PCM Data Out> # - GPIO22: # - GPIO23: # - GPIO24: "LCD RST <ReSeT control>" # - GPIO25: "Servo 1 control" # - GPIO26: "LCD LED <backlight LED control>" <for input> # - GPIO27: "LCD DC <Data/Command (NOT MOSI!)>" <for output>
Raspberry Piの40ピン構成：
# 40-pins configuration of Raspberry Pi: # 3V3 (1) (2) 5V # GPIO2 (3) (4) 5V # GPIO3 (5) (6) GND # GPIO4 (7) (8) GPIO14 # GND (9) (10) GPIO15 # GPIO17 (11) (12) GPIO18 # GPIO27 (13) (14) GND # GPIO22 (15) (16) GPIO23 # 3V3 (17) (18) GPIO24 # GPIO10 (19) (20) GND # GPIO9 (21) (22) GPIO25 # GPIO11 (23) (24) GPIO8 # GND (25) (26) GPIO7 # GPIO0 (27) (28) GPIO1 # GPIO5 (29) (30) GND # GPIO6 (31) (32) GPIO12 # GPIO13 (33) (34) GND # GPIO19 (35) (36) GPIO16 # GPIO26 (37) (38) GPIO20 # GND (39) (40) GPIO21
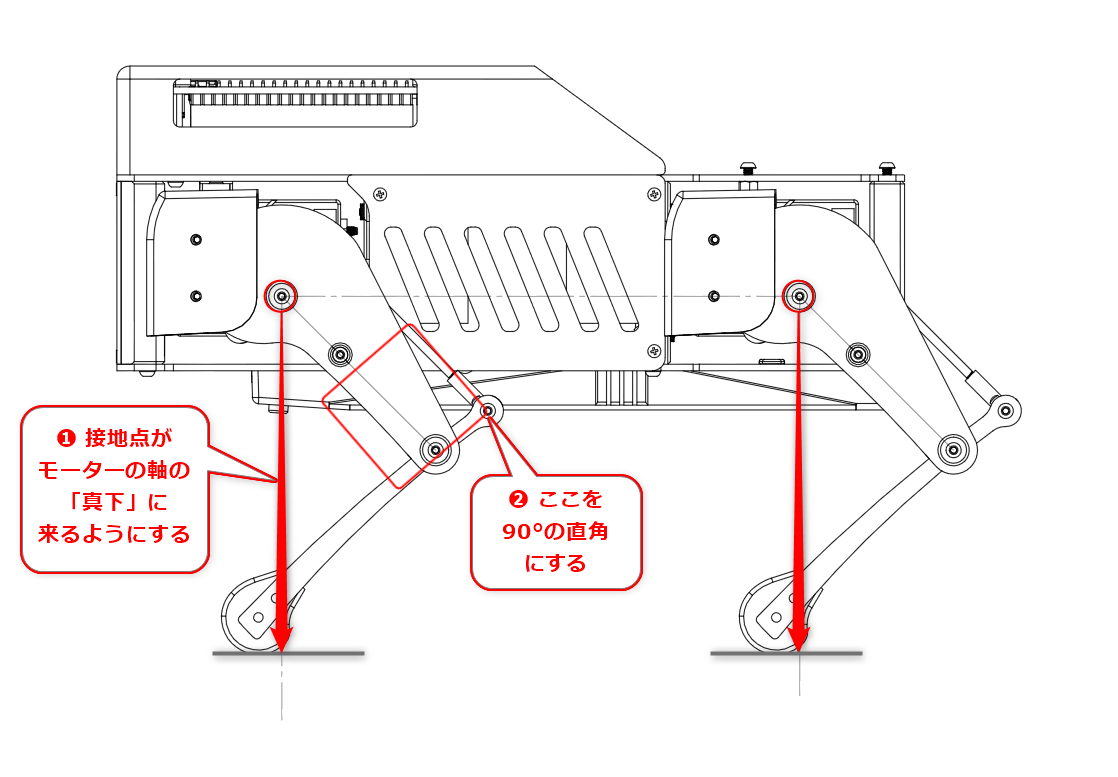
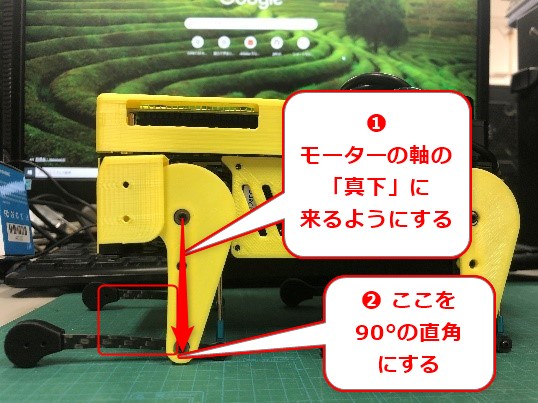
ミニぷぱのROS版を触っていて、少し知見がたまってきています。
非常にニッチだと思いますが、ミニぷぱのROS版をPS4版のように扱えないと感じる人も多いかと思うので、個人的に知っている内容を書いておきます。誰かに役立つといいけど。
※書く必要もないと思いますが念のため。この記事の通りに実施して何か起きた場合の責任は筆者および本サイトは負いません。自己責任でお願いします。
PS4版では起動時に鳴くので起動が分かりやすいです。なぜかROS版では実装してくれていません（もしかしたら最新版では対応済みかもしれません。確認していません）。
鳴き声の音声はこちらにあります： github.com
これを再生するだけです。再生コマンドはmpg123 /home/ubuntu/Music/power_on.mp3にようになります。このコマンド実行を、起動時のrc.localサービスで実行してもらいます：
github.com
rc.localファイルは、
/home/ubuntu/minipupper_ros_bsp/mangdang/System/rc.localにあります。私のrc.localファイルの中身は以下のようになっています。個人的にカスタマイズを試しまくっているので元と違うかもしれません。
#!/bin/bash
#
# 1.Initialize power switch and pwm units
# 2.start lcd
#
# Copyright (c) 2020, Mangdang Technology Co., Limited
#
#
#remove bluebooth cache
# sudo rm /var/lib/bluetooth/* -rf
# sleep 2
# get hardware version
# echo 27 > /sys/class/gpio/export
# echo in > /sys/class/gpio/gpio27/direction
# hw_version_io=`cat /sys/class/gpio/gpio27/value`
# echo 27 > /sys/class/gpio/unexport
# if [ "$hw_version_io" == "1" ]; then
# sudo echo "P1" > /home/ubuntu/.hw_version
# else
# sudo echo "MP" > /home/ubuntu/.hw_version
# fi
#export pwm channel
for i in $(seq 0 15)
do
sudo echo $i > /sys/class/pwm/pwmchip0/export
sudo echo 4000000 > /sys/class/pwm/pwmchip0/pwm$i/period
sudo chmod 777 /sys/class/pwm/pwmchip0/pwm$i/duty_cycle
done
# init the Bluetooth
# sudo hciattach /dev/ttyAMA0 bcm43xx 115200 noflow -
# sleep 8
# sudo hciattach /dev/ttyAMA0 bcm43xx 115200 noflow -
# sleep 2
# init lcd
#python3 /home/ubuntu/minipupper_ros_bsp/mangdang/LCD/lcd_init.py
# set cpu performance
# Set the Frequency Governor to Performance (run CPU at maximum frequency) which determines the frequency policy. Default is On-Demand
# cat /sys/devices/system/cpu/cpu0/cpufreq/scaling_available_governors
# conservative ondemand userspace powersave performance schedutil が利用可能
echo performance > /sys/bus/cpu/devices/cpu0/cpufreq/scaling_governor
# show wake-up-face (& means background job)
su ubuntu -l -c "python3 /home/ubuntu/minipupper_ros_bsp/mangdang/LCD/wake-up-face.py" &
# play sound (& means background job)
su ubuntu -l -c "mpg123 /home/ubuntu/Music/power_on.mp3" &
exit 0
音声コマンドは最後に実行しているsu ubuntu -l -c "mpg123 /home/ubuntu/Music/power_on.mp3" &ですね。/home/ubuntu/Music/ディレクトリに音声ファイルを配置しました。
このrc.localサービスを有効にするには、以下のコマンドを実行してください。
# Install mangdang wake-up service cd /home/ubuntu/minipupper_ros_bsp/mangdang/System sudo bash install.sh sudo reboot
顔もアニメーションさせたりいろいろとできるのですが、PS4版で動くとアニメーションするようなコードになっていたと思います。それを実装するのは面倒なので、取りあえず起動時にlogo用の顔（黄色と黒色が反転した顔）を表示させるようにしてみましょう。手間を省くため、上記と同じrc.localサービスを利用しました。
上のコードにあるsu ubuntu -l -c "python3 /home/ubuntu/minipupper_ros_bsp/mangdang/LCD/wake-up-face.py" &がその部分です。Pythonスクリプトを呼び出しています。そのスクリプトコードは以下の通りです。
import os
import sys
from PIL import Image
sys.path.append('/home/ubuntu/minipupper_ros_bsp')
sys.path.extend([os.path.join(root, name) for root, dirs, _ in os.walk('/home/ubuntu/minipupper_ros_bsp') for name in dirs])
# sys.path.append('/home/ubuntu/minipupper_ros_bsp/mangdang')
# sys.path.extend([os.path.join(root, name) for root, dirs, _ in os.walk('/home/ubuntu/minipupper_ros_bsp/mangdang') for name in dirs])
# from LCD.ST7789 import ST7789
from mangdang.LCD.ST7789 import ST7789
cartoons_folder = '/home/ubuntu/Pictures/'
disp = ST7789()
def main():
""" To show wake-up-face
"""
# Firstly, show logo
#init st7789 device
global disp
disp.begin()
disp.clear()
image=Image.open(cartoons_folder + 'logo.png')
image.resize((320,240))
disp.display(image)
main()
####
#### run this script
####
# python3 /home/ubuntu/minipupper_ros_bsp/mangdang/LCD/wake-up-face.py
顔画像はこちらにあります： github.com
これらの画像ファイルを/home/ubuntu/Pictures/ディレクトリに配置しました。
仕組みさえ分かってしまえば特に難しいとろころはないのではないかと思います。その仕組みを説明する資料がないんですよね...。こんな感じでプログラミング次第で何でもできます。
ヒントとして、ROS版のこういったプログラム関連とそのインストール用ファイルは、
/home/ubuntu/minipupper_ros_bsp/mangdangにまとめられています。それに対応するGitHubリポジトリが以下だと思います。
https://github.com/mangdangroboticsclub/minipupper_ros_bspまた、ROS用のコマンドなど（ワークスペース）は、
/home/ubuntu/catkin_wsというディレクトに入っています。それに対応するGitHubリポジトリが以下だと思います。
https://github.com/mangdangroboticsclub/minipupper_rosついでにバッテリー電池不足時に鳴かせる方法も紹介しておきます。起動時に鳴かせる方法と基本的な考え方は同じです。電池がなくなったらsu ubuntu -l -c "mpg123 /home/ubuntu/Music/low_power.mp3"を実行するだけです。
バッテリー電池は/home/ubuntu/minipupper_ros_bsp/mangdang/FuelGauge/battery_monitorサービスで対応できます。私のbattery_monitorファイルの中身は以下のようになっています。
#!/bin/bash
#
# Copyright (c) 2021, Mangdang Technology Co., Limited
#
# IO Mapping configuration
IO_MAP=(
25 1 # Servo 1 control for v2 board - on
21 1 # Servo 2 control for v2 board - on
#26 1 # LCD LED <backlight LED control> - on
#24 0 # LCD RST <ReSeT control> - off
#27 0 # LCD DC <Data/Command (NOT MOSI!)> - off
)
# Set the above Configuration
function io_init(){
len=${#IO_MAP[@]}
for((i=0;i<len;i+=2))
do
io=${IO_MAP[i]}
val=${IO_MAP[i+1]}
echo $io > /sys/class/gpio/export
echo out > /sys/class/gpio/gpio$io/direction
echo $val > /sys/class/gpio/gpio$io/value
done
}
# init IO
io_init
sleep 1
chmod 777 /sys/class/gpio/gpio24/value
chmod 777 /sys/class/gpio/gpio27/value
chmod 777 /dev/spidev0.0
#Power monitor
while true
do
current_voltage=`cat /sys/class/power_supply/max1720x_battery/voltage_now`
if [ $current_voltage -le 6500 ]; then
echo 0 > /sys/class/gpio/gpio25/value
echo 0 > /sys/class/gpio/gpio21/value
su ubuntu -l -c "mpg123 /home/ubuntu/Music/low_power.mp3"
fi
sleep 8
done
このコード内のcat /sys/class/power_supply/max1720x_battery/voltage_nowで電圧をチェックし、電圧が6500未満になると、su ubuntu -l -c "mpg123 /home/ubuntu/Music/low_power.mp3"で音声ファイルを鳴らし続けています。PS4版のコードそのもののコードになっています。仕組みは簡単です。
ちなみにROS版の元々のコードでは、バッテリー側のブザー音を鳴らす内容になっていたと思います。音声ファイルの鳴き声の方が気分が乗りますよね。
このbattery_monitorサービスを有効にするには、以下のコマンドを実行してください。
# Install mangdang power-on service cd /home/ubuntu/minipupper_ros_bsp/mangdang/FuelGauge sudo bash install.sh sudo reboot
ミニぷぱに付属のバッテリーでは、このように電圧をチェックできますが、人が見る場合、「電池があと何％？」と見た方が分かりやすいですよね。これを調べるには、
cat /sys/class/power_supply/max1720x_battery/capacity
というコマンドを実行すればよいです。実開発作業ではGUIを見ずにSSHでVisual Studio Codeから触ることが多いのではないかと思いますが、このコマンドは便利ですよ。
（走り書きで見直してないです以上です。読む人も限られると思うので最小コストで。）
GUIログイン画面からCUI切り替えるためのキー入力は、ネット上にたくさん情報があるはずだけど、必要なときに検索しても必要な情報が探し出しづらくて困ったので、自分でも備忘録を残して置くことにしました。
［Ctrl］＋［Alt］＋［F1］キー
［Alt］＋［F7］キー
